What Do You Know if You Have Lengths of Sides of Triangle

Eugene is a qualified control/instrumentation engineer Bsc (Eng) and has worked every bit a developer of electronics & software for SCADA systems.

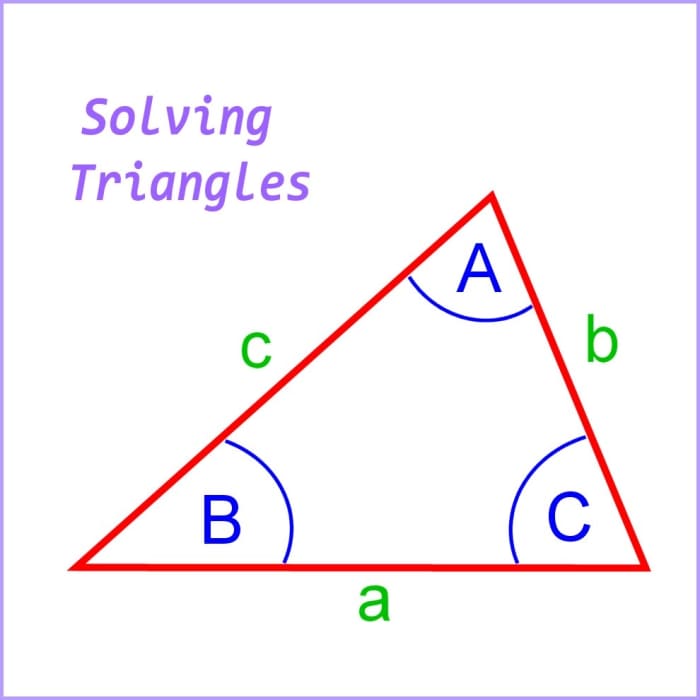
Solving triangles

© Eugene Brennan

Trigonometry and Triangles

In this tutorial, you'll learn about trigonometry which is a branch of mathematics that covers the relationship between the sides and angles of triangles.

We'll notice out nigh:

• Polygons and the Definition of a Triangle
• The Basic Facts About Triangles
• The Triangle Inequality Theorem
• Different Types of Triangles
• Using the Greek Alphabet for Equations
• Sine, Cosine and Tangent
• Pythagoras's Theorem
• The Sine and Cosine Rules
• How to Piece of work Out the Sides and Angles of a Triangle
• Measuring Angles
• How to Calculate the Area of a Triangle

What Is a Triangle?

By definition, a triangle is a polygon with iii sides.

Polygons are airplane shapes with several direct sides. "Plane" merely means they're flat and two-dimensional. Other examples of polygons include squares, pentagons, hexagons and octagons. The word plane originates from the Greek polús meaning "many" and gōnía significant "corner" or "angle." So polygon means "many corners." A triangle is the simplest possible polygon, having simply three sides.

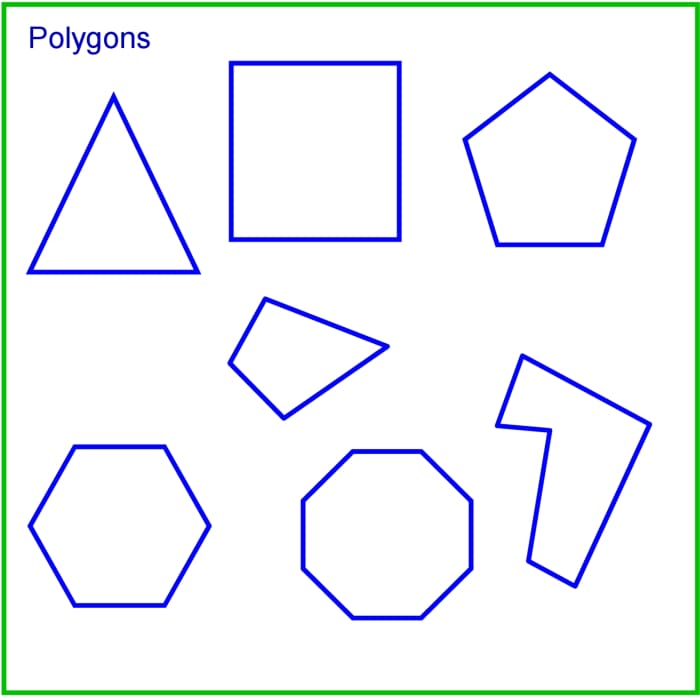
Polygons with different numbers of sides. Regular polgons have sides the aforementioned length.

© Eugene Brennan

Bones Facts About Triangles

• A triangle is a polygon with 3 sides.
• All the internal angles add upwards to a total of 180 degrees.
• The angle between two sides can exist annihilation from greater than 0 to less than 180 degrees.
• The bending between 2 sides can't be 0 or 180 degrees, because the triangle would then go straight lines. (These are called degenerate triangles).
• Similar triangles have the same angles, only different length sides.

The Symbol for Degrees

Degrees tin be written using the symbol º. So, 45º means 45 degrees.

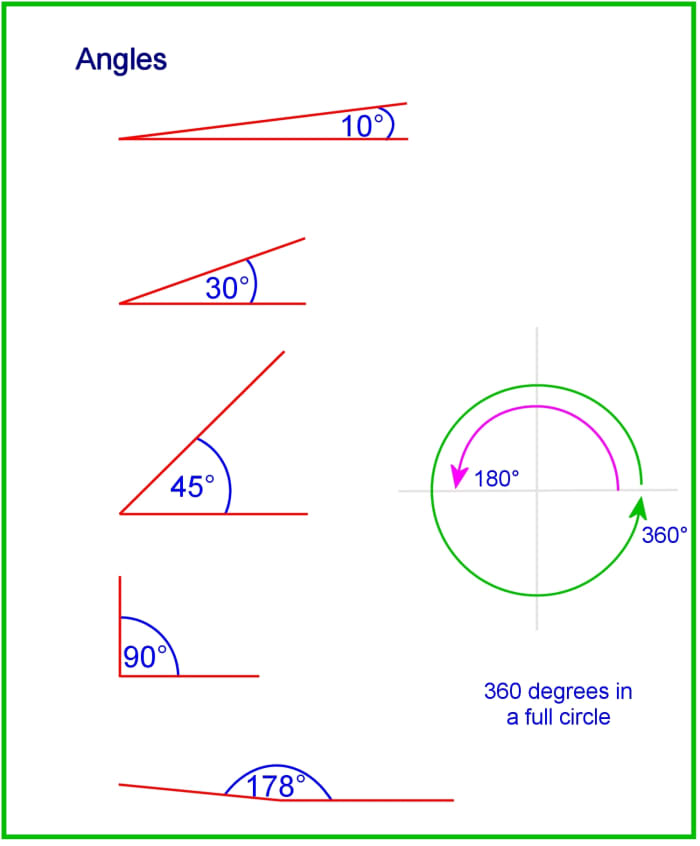
Angles of a triangle range from 0 to less than 180 degrees.

© Eugene Brennan

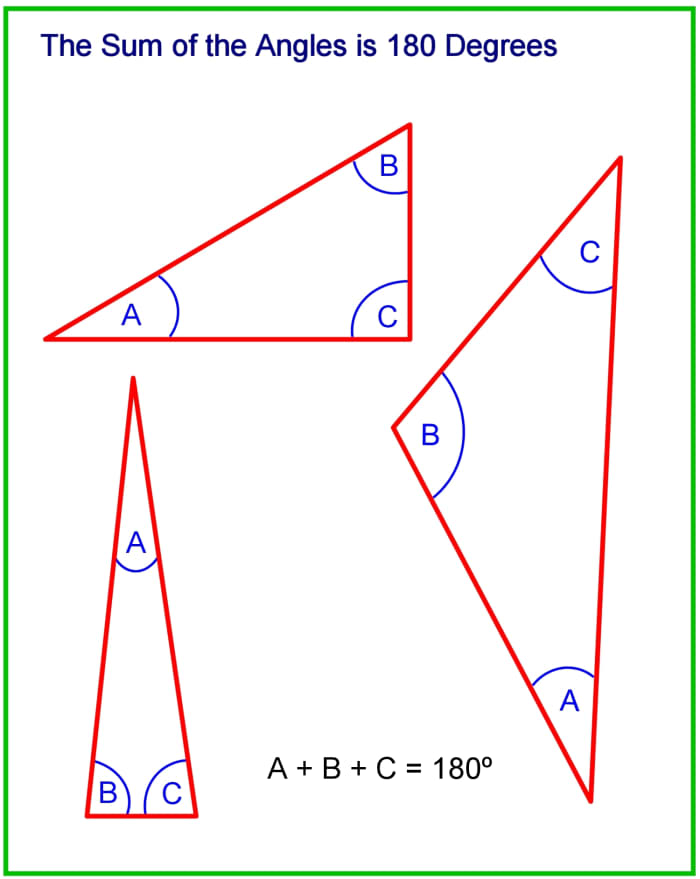
No matter what the shape or size of a triangle, the sum of the 3 internal angles is 180

© Eugene Brennan

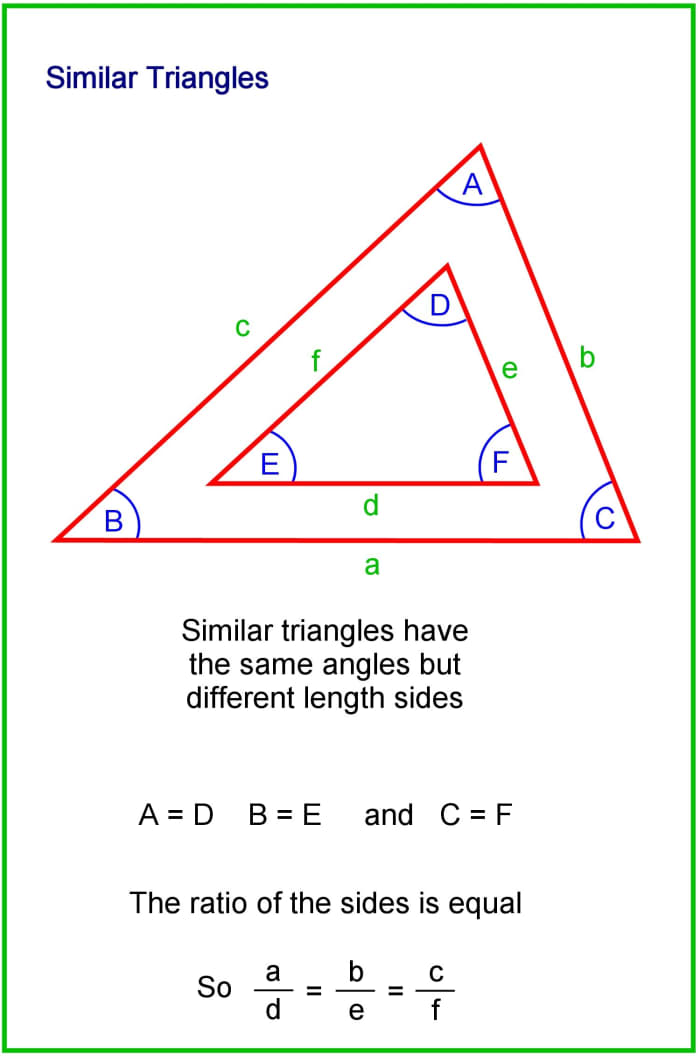
Similar triangles take the same angles but different length sides.

© Eugene Brennan

What Is the Triangle Inequality Theorem?

This states that the sum of any ii sides of a triangle must be greater than or equal to the remaining side.

What Are the Different Types of Triangles?

Before nosotros learn how to piece of work out the sides and angles of a triangle, it's important to know the names of the different types of triangles. The classification of a triangle depends on 2 factors:

• The length of a triangle's sides
• The angles of a triangle's corners

Read More than From Owlcation

Types of Triangles Past Sides and Angles

Y'all can allocate a triangle either by side length or internal bending.

Types of triangles by length of sides.

Blazon of Triangle by Lengths of Sides	Clarification
Isosceles	An isosceles triangle has ii sides of equal length, and 1 side that is either longer or shorter than the equal sides. Angle has no bearing on this triangle type.
Equilateral	All sides and angles are equal in length and degree.
Scalene	All sides and angles are of different lengths and degrees.

Types of triangles past angle.

Type of Triangle by Internal Bending	Description
Correct (right angled)	One angle is ninety degrees.
Acute	Each of the iii angles measure less than xc degrees.
Obtuse	Ane bending is greater than 90 degrees.

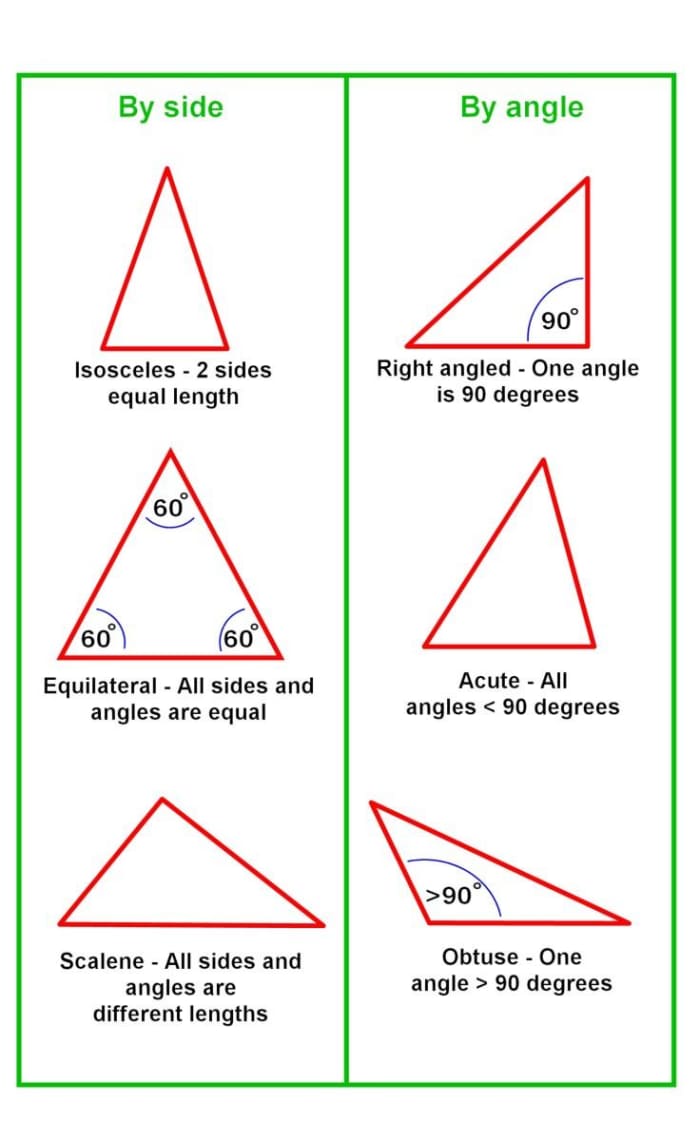
Triangles classified by side and angles.

© Eugene Brennan

Using the Greek Alphabet for Equations

Some other topic that we'll briefly cover earlier we delve into the mathematics of solving triangles is the Greek alphabet.

In scientific discipline, mathematics, and applied science many of the 24 characters of the Greek alphabet are borrowed for utilise in diagrams and for describing certain quantities.

You may take seen the character μ (mu) represent micro as in micrograms μg or micrometers μm. The uppercase letter Ω (omega) is the symbol for ohms in electric engineering. And, of course, π (pi) is the ratio of the circumference to the diameter of a circle.

In trigonometry, the characters θ (theta) and φ (phi) are oft used for representing angles.

Letters of the Greek alphabet.

© Eugene Brennan

How Do Yous Find the Sides and Angles of a Triangle?

There are several methods for working out the sides and angles of a triangle. To observe the length or bending of a triangle, 1 tin use formulas, mathematical rules, or the fact that the angles of all triangles add up to 180 degrees.

Tools to discover the sides and angles of a triangle

• Pythagoras's theorem
• Sine rule
• Cosine rule
• The fact that all angles add up to 180 degrees

Pythagoras's Theorem (The Pythagorean Theorem)

Pythagoras's theorem uses trigonometry to notice the longest side (hypotenuse) of a right triangle (right angled triangle in British English). It states that for a correct triangle:

The square on the hypotenuse equals the sum of the squares on the other two sides.

If the sides of a triangle are a, b and c and c is the hypotenuse, Pythagoras's Theorem states that:

c ² = a ² + b ²

c = √(a² + b ²)

The hypotenuse is the longest side of a right triangle, and is located opposite the right angle.

So, if you know the lengths of two sides, all y'all have to do is foursquare the two lengths, add the consequence, and so take the square root of the sum to become the length of the hypotenuse.

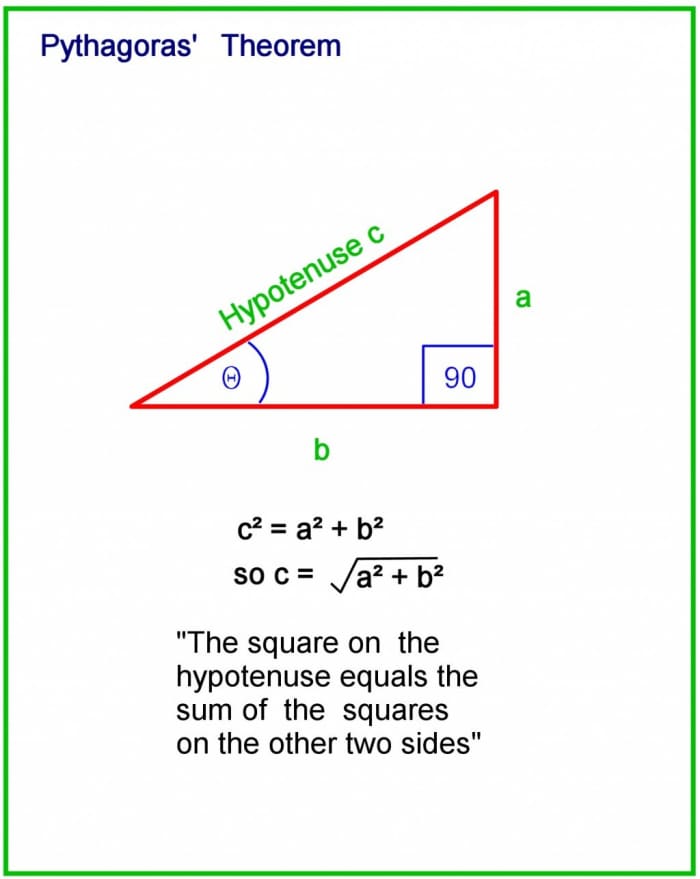
Pythagoras's Theorem

© Eugene Brennan

Example Trouble Using the Pythagorean Theorem

The sides of a triangle are three and four units long. What is the length of the hypotenuse?

Call the sides a, b, and c. Side c is the hypotenuse.

a = three
b = 4

c = Unknown

So, according to the Pythagorean theorem:

cⁱⁱ = a² + b ^two

So, c² = 3² + 4ⁱⁱ = ix + 16 = 25

c = √25

c = five

How Exercise You Measure Angles?

Yous can utilise a protractor or a digital angle finder like this one from Amazon. These are useful for DIY and construction if yous need to measure an bending between ii sides, or transfer the angle to some other object. You can utilise this as a replacement for a bevel gauge for transferring angles e.1000. when marking the ends of rafters before cutting. The rules are graduated in inches and centimetres and angles can be measured to 0.1 degrees.

Annotation that this isn't suitable as a technical drawing instrument considering the hub won't sit apartment on paper unlike a protractor. Also since it's fabricated of stainless steel, it has pointed corners which may be sharp and therefore isn't suitable for immature children.

You can draw and measure out angles with a protractor.

© Eugene Brennan

Sine, Cosine and Tangent of an Angle

A right triangle has one angle measuring 90 degrees. The side opposite this angle is known as the hypotenuse (another name for the longest side). The length of the hypotenuse tin be discovered using Pythagoras's theorem, just to observe the other ii sides, sine and cosine must exist used. These are trigonometric functions of an bending.

In the diagram below, one of the angles is represented by the Greek letter θ. (pronounced "the - ta"). Side a is known as the "opposite" side and side b is chosen the "side by side" side because of their positions relative to the bending θ.

The vertical lines "||" around the words below hateful "length of."

Then sine, cosine and tangent are defined as follows:

sine θ = |opposite side| / |hypotenuse|

cosine θ = |side by side side| / |hypotenuse|

tan θ = |opposite side| / |adjacent side|

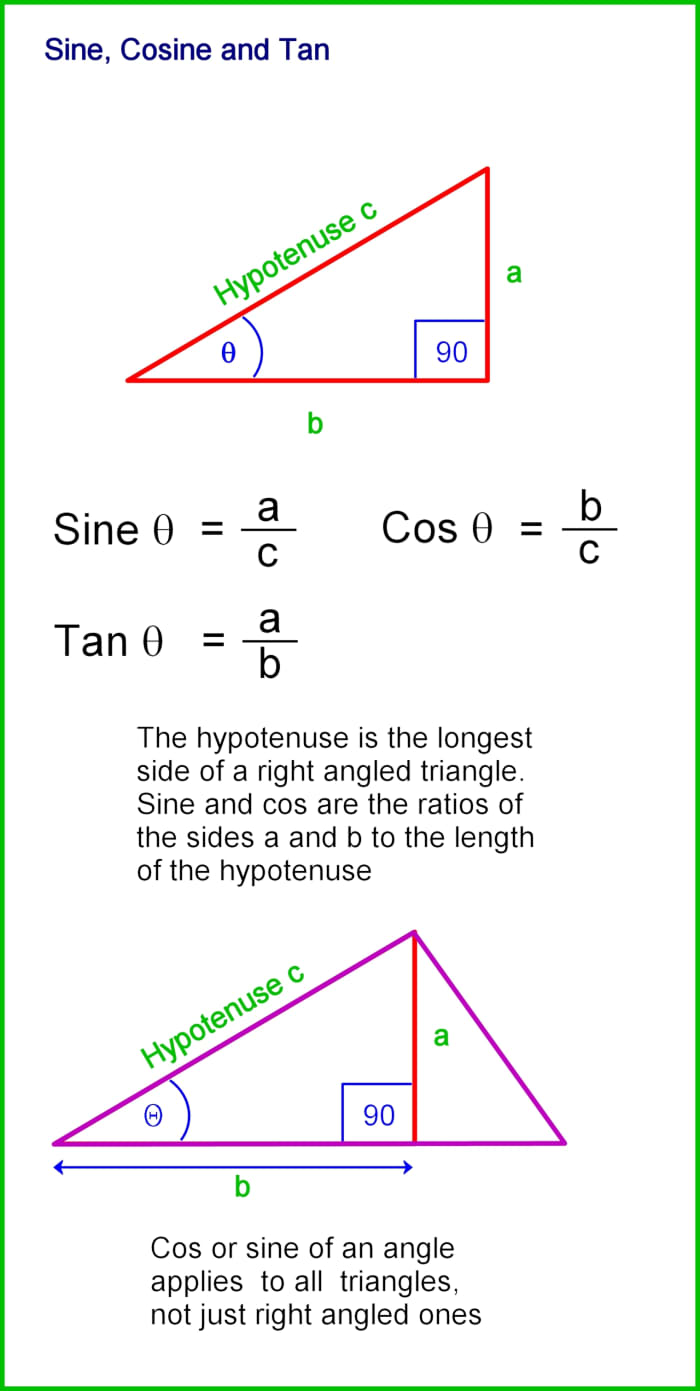
Sine, cosine and tan.

© Eugene Brennan

Sine and cosine apply to an angle, any angle, so information technology's possible to have two lines meeting at a betoken and to evaluate sine or cosine for that angle even though there's no triangle every bit such. Withal, sine and cosine are derived from the sides of an imaginary right triangle superimposed on the lines.

For instance, in the 2d diagram above, the imperial triangle is scalene not right angled. However, you lot can imagine a right-angled triangle superimposed on the purple triangle, from which the opposite, adjacent and hypotenuse sides can be determined.

Over a range 0 to 90 degrees, sine ranges from 0 to 1, and cosine ranges from 1 to 0.

Call back, sine and cosine merely depend on the bending, non the size of the triangle. Then if the length a changes in the diagram to a higher place when the triangle changes in size, the hypotenuse c too changes in size, just the ratio of a to c remains constant. They are like triangles.

Sine, cosine and tangent are oft abbreviated to sin, cos and tan respectively.

The Sine Rule

The ratio of the length of a side of a triangle to the sine of the angle contrary is constant for all iii sides and angles.

Then, in the diagram below:

a / sine A = b / sine B = c / sine C

Now, you tin can check the sine of an bending using a scientific estimator or expect it up online. In the one-time days before scientific calculators, we had to look up the value of the sine or cos of an bending in a volume of tables.

The opposite or reverse part of sine is arcsine or "inverse sine", sometimes written as sin^-1 . When you lot check the arcsine of a value, you're working out the angle which produced that value when the sine function was operated on it. So:

sin (30º) = 0.5 and sin ^-1 (0.5) = 30º

When should the sine rule be used?

The length of one side and the magnitude of the angle opposite is known. Then, if any of the other remaining angles or sides are known, all the angles and sides tin be worked out.

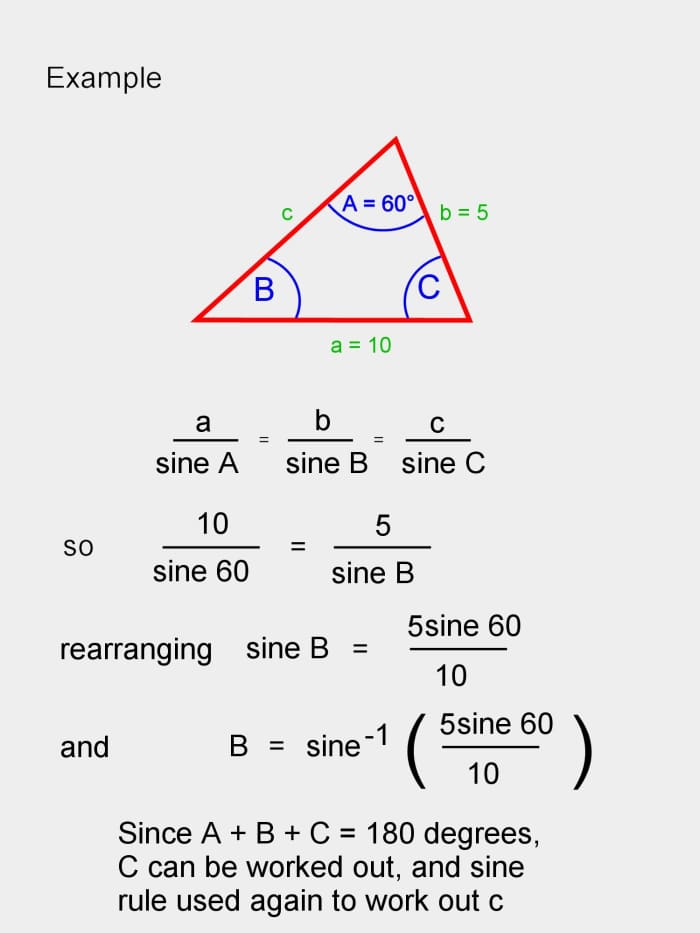
Example showing how to utilize the sine rule to calculate the unknown side c.

© Eugene Brennan

The Cosine Rule

For a triangle with sides a, b, and c, if a and b are known and C is the included angle (the angle between the sides), C tin be worked out with the cosine rule. The formula is as follows:

c = a ⁱⁱ + b ² - 2ab cos C

When should the cosine rule be used?

1. You know the lengths of the two sides of a triangle and the included bending. You tin can then piece of work out the length of the remaining side using the cosine rule.
2. You know all the lengths of the sides merely none of the angles.

So, by rearranging the cosine rule equation:

C = arccos ((a ² + b ⁱⁱ - c ²) / iiab)

The other angles tin be worked out similarly.

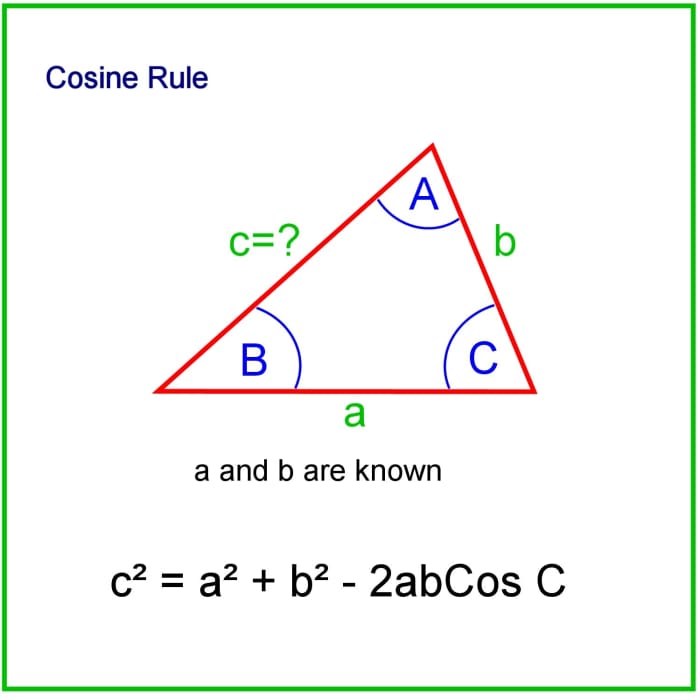
The cosine rule.

© Eugene Brennan

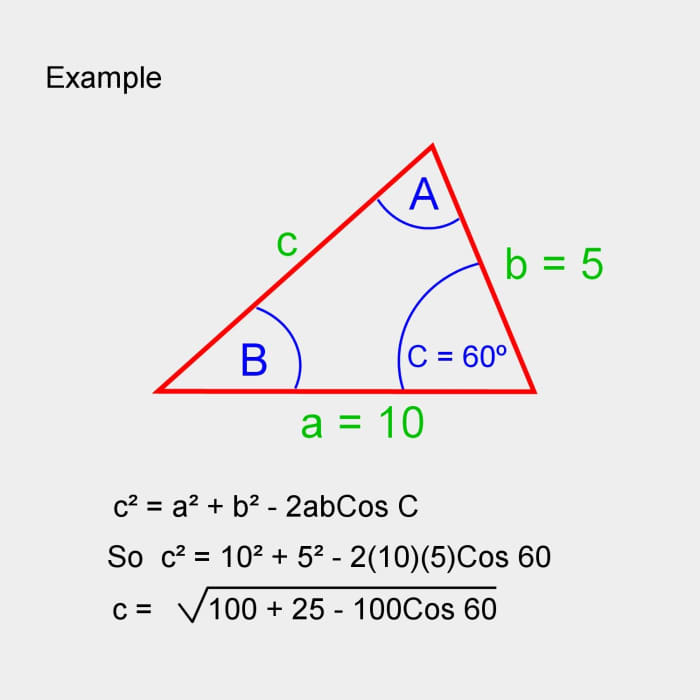
Example using the cosine rule.

© Eugene Brennan

How to Find the Angles of a Triangle Knowing the Ratio of the Side Lengths

If you know the ratio of the side lengths, yous can use the cosine dominion to piece of work out 2 angles then the remaining angle can be found knowing all angles add to 180 degrees.

Example:

A triangle has sides in the ratio v:7:viii. Observe the angles.

Answer:

So call the sides a, b and c and the angles A, B and C and assume the sides are a = 5 units, b = 7 units and c = 8 units. Information technology doesn't matter what the actual lengths of the sides are considering all similar triangles have the aforementioned angles. And then if we work out the values of the angles for a triangle which has a side a = 5 units, information technology gives the states the issue for all these similar triangles.

Use the cosine rule. And then c ² = a ² + b ² - twoab cos C

Substitute for a,b and c giving:

8² = 5² + seven² - 2(5)(7) cos C

Working this out gives:

64 = 25 + 49 - 70 cos C

Simplifying and rearranging:

cos C = one/vii and C = arccos(1/7).

Yous can use the cosine rule once more or sine rule to find a second angle and the tertiary angle tin can be institute knowing all the angles add to 180 degrees.

How to Become the Area of a Triangle

At that place are 3 methods that can be used to discover the expanse of a triangle.

Method one. Using the perpendicular meridian

The area of a triangle tin can be determined by multiplying one-half the length of its base by the perpendicular height. Perpendicular means at right angles. Only which side is the base? Well, y'all can use any of the three sides. Using a pencil, you can work out the surface area past drawing a perpendicular line from one side to the reverse corner using a set foursquare, T-square, or protractor (or a carpenter'south square if you're constructing something). Then, measure the length of the line and apply the following formula to get the expanse:

Area = 1/2ah

"a" represents the length of the base of the triangle and "h" represents the height of the perpendicular line.

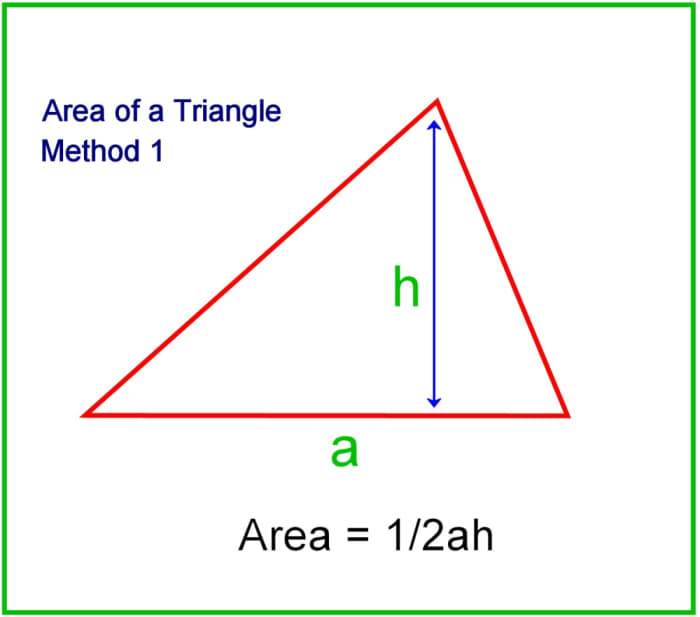
Working out the expanse of a triangle from the base lengtth and perpendicular top.

© Eugene Brennan

Method 2. Using side lengths and angles

The simple method in a higher place requires yous to really measure out the elevation of a triangle. If y'all know the length of two of the sides and the included bending, you can work out the area analytically using sine and cosine (encounter diagram below).

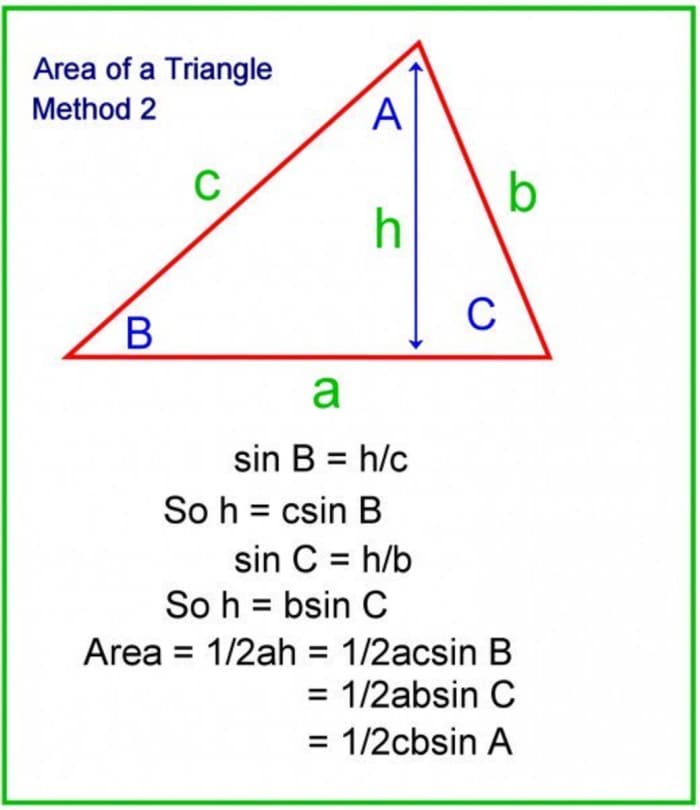
Working out the area of a triangle from the lengths of 2 sides and the sine of the included bending.

© Eugene Brennan

Method 3. Use Heron's formula

All you demand to know are the lengths of the three sides.

Expanse = √(south(s - a)(s - b)(south - c))

Where s is the semiperimeter of the triangle

southward = (a + b + c)/2

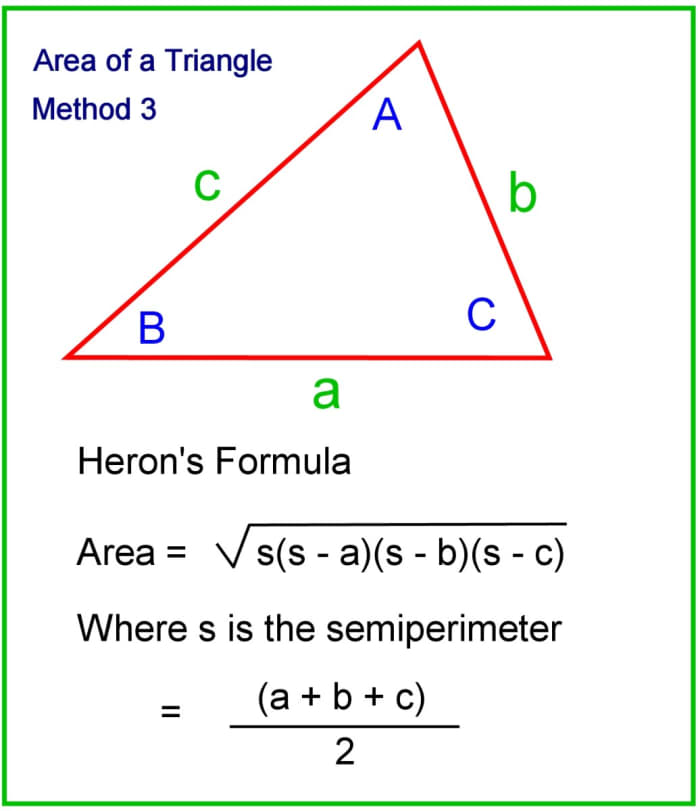
Using Heron'southward formua to piece of work out the area of a triangle.

© Eugene Brennan

Summary

If you lot've made it this far, you've learned numerous helpful methods to discover different aspects of a triangle. With all this information, you may be confused as to when you should use which method. The table below should help you identify which rule to use depending on the parameters you lot have been given.

Discover the Angles and Sides of a Triangle: Which Rule Practice I Use?

A summary of how to piece of work out angles and sides of a triangle.

Known Parameters	Triangle Type	Rule to Use
Triangle is right and I know length of two sides.	SSS after Pythagoras'south Theorem used	Use Pythagoras's Theorem to work out remaining side and sine rule to work out angles.
Triangle is right and I know the length of one side and one bending	AAS after 3rd angle worked out	Use the trigonometric identities sine and cosine to work out the other sides and sum of angles (180 degrees) to work out remaining angle.
I know the length of two sides and the angle between them.	SAS	Use the cosine rule to work out remaining side and sine dominion to work out remaining angles.
I know the length of 2 sides and the bending opposite one of them.	SSA	Use the sine rule to work out remaining angles and side.
I know the length of one side and all 3 angles.	AAS	Use the sine rule to work out the remaining sides.
I know the lengths of all three sides	SSS	Utilise the cosine rule in opposite to work out each bending. C = Arccos ((a² + b² - c²) / 2ab)
I know the length of a side and the angle at each end	AAS	Sum of 3 angles is 180 degrees so remainging bending tin can be calculated. Use the sine rule to piece of work out the two unknown sides
I know the length of a side and one bending		You demand to know more information, either one other side or one other angle. Thes exception is if the known angle is in a rightangled triangle and non the right angle.

FAQs Near Triangles

Below are some frequently asked questions about triangles.

What do the angles of a triangle add up to?

The interior angles of all triangles add together upward to 180 degrees.

What Is the hypotenuse of a triangle?

The hypotenuse of a triangle is its longest side.

What do the sides of a triangle add up to?

The sum of the sides of a triangle depends on the individual lengths of each side. Dissimilar the interior angles of a triangle, which always add up to 180 degrees

How do yous calculate the expanse of a triangle?

To calculate the expanse of a triangle, only use the formula:

Area = one/2ah

"a" represents the length of the base of the triangle. "h" represents its meridian, which is discovered past drawing a perpendicular line from the base to the superlative of the triangle.

How practice you lot find the third side of a triangle that Is not right?

If you lot know two sides and the angle betwixt them, use the cosine rule and plug in the values for the sides b, c, and the angle A.

Next, solve for side a.

Then use the angle value and the sine rule to solve for angle B.

Finally, apply your knowledge that the angles of all triangles add up to 180 degrees to notice angle C.

How do you lot find the missing side of a right angled triangle?

Use the Pythagorean theorem to find the missing side of a triangle. The formula is as follows:

c² = a² + b ²

c = √(a ² + b ²)

What is the name of a triangle with two equal sides?

A triangle with two equal sides and one side that is longer or shorter than the others is called an isosceles triangle.

What is the cosine formula?

This formula gives the square on a side opposite an angle, knowing the angle between the other two known sides. For a triangle, with sides a, b and c and angles A, B and C the iii formulas are:

a ^two = b ⁱⁱ + c ² - 2bc cos A

or

b ² = a ² + c ² - iiair conditioning cos B

or

c ² = a ² + b ² - twoab cos C

How to figure out the sides of a triangle if I know all the angles?

You lot demand to know at least one side, otherwise, y'all tin can't work out the lengths of the triangle. In that location'due south no unique triangle that has all angles the same. Triangles with the same angles are like but the ratio of sides for any 2 triangles is the same.

How to work out the sides of a triangle if I know all the sides?

Apply the cosine rule in reverse.
The cosine rule states:

c ^two = a ² + b ² - iiab cos C

Then, by rearranging the cosine rule equation, you can piece of work out the angle

C = arccos ((a ² + b ² - c ⁱⁱ) / 2ab)

and

B

= arccos ((a ²+ c ⁱⁱ - b ²) / 2air-conditioning)

The 3rd angle A is (180 - C - B)

How to find the perimeter of a triangle

Finding the perimeter of a triangle is a straightforward functioning. The perimeter is equivalent to the added lengths of all three sides.

perimeter = a + b + c

How to detect the elevation of a triangle

Finding the height of a triangle is like shooting fish in a barrel if you take the triangle'south area. If you're given the expanse of the triangle:

height = ii 10 area / base

If yous don't take the area, but only accept the side lengths of the triangle, use the post-obit:

elevation = 0.5 x √ ((a + b + c)(-a + b + c)(a - b + c)(a + b - c)) / b

If yous but have two sides and the angle between them, try this formula:

surface area = 0.5 (a)(b)(sin(γ)), so

tiptop = area(sin(γ))

Triangles in the Real World

A triangle is the most basic polygon and can't be pushed out of shape hands, unlike a square. If yous expect closely, triangles are used in the designs of many machines and structures because the shape is so strong.

The strength of the triangle lies in the fact that when whatever of the corners are conveying weight, the side opposite acts every bit a tie, undergoing tension and preventing the framework from deforming. For example, on a roof truss, the horizontal ties provide strength and prevent the roof from spreading out at the eaves.

The sides of a triangle can as well human action as struts, only in this case, they undergo pinch. An example is a shelf subclass or the struts on the underside of an aeroplane fly or the tail fly itself.

How to Implement the Cosine Rule in Excel

Y'all tin implement the cosine rule in Excel using the ACOS Excel role to evaluate arccos. This allows the included angle to be worked out, knowing all iii sides of a triangle.

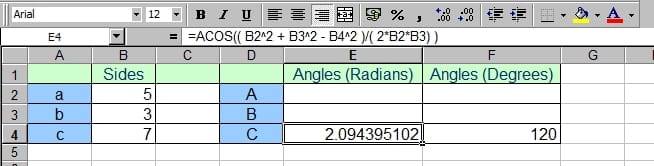
Using the Excel ACOS function to work out an angle, knowing iii sides of a triangle. ACOS returns a value in radians.

© Eugene Brennan

How to Summate Arc Length of a Circumvolve, Segment and Sector Surface area

This content is accurate and true to the best of the writer's knowledge and is non meant to substitute for formal and individualized advice from a qualified professional.

Questions & Answers

Question: How do you find the remaining sides of a triangle if you have merely one angle and one side given?

Answer: You need to have more information. Then either one side and the two angles at each end or two sides and the angle between them.

You lot can prove this to yourself past drawing out the single side and angle and seeing how you tin depict as many unlike shaped triangles as you desire.

Question: How practise I observe the value if all three sides of a scalene triangle are unknown?

Answer: If all the sides are unknown, you lot can't solve the triangle. Yous need to know at least two angles and i side, or two sides and ane angle, or one side and one angle if the triangle is a right-angled triangle.

Question: What is the formula for finding what an equilateral triangle of side a, b and c is?

Reply: Since the triangle is equilateral, all the angles are sixty degrees. However, the length of at least ane side must exist known. Once you know that length, since the triangle is equilateral, you know the length of the other sides considering all sides are of equal length.

Question: How would you solve this problem: The bending of elevation of the acme of a tree from bespeak P west of the tree is 40 degrees. From a second point Q due eastward of the tree, the bending of height is 32 degrees. If the distance between P and Q is 200m, find the top of the tree, correct to iv pregnant figures?

Answer: One bending is 40 degrees, the other bending is 32 degrees, therefore the tertiary angle opposite the base PQ is 180 - (32 + xl) = 108 degrees.

Yous know one side of the triangle has length PQ = 200 one thousand

A right angled triangle is formed between point P, the tiptop of the tree and its base and as well bespeak Q, the top of the tree and its base.

The best way to solve is to find the hypotenuse of one of the triangles.

So utilize the triangle with vertex P.

Call the bespeak at the top of the tree T

Call the height of the tree H

The angle formed betwixt sides PT and QT was worked out as 108 degrees.

Using the Sine Rule, PQ / Sin(108) = PT/ Sin(32)

So for the right angled triangle we chose, PT is the hypotenuse.

Rearranging the equation above

PT = PQSin(32) / Sin(108)

Sin(40) = H / PT

So H = PTSin(40)

Substituting the value for the hypotenuse PT we calculated above gives

H = (PQSin(32) / Sin(108)) 10 Sin(forty)

= PQSin(32)Sin(forty)/Sin(108)

= 71.63 m

Question: How practice I find the missing side of a triangle when only its height is known?

Respond: Use Pythagoras's Theorem. Add the sine, cosine and tan relationships between angles and the hypotenuse of the triangle to work out the remaining side.

Question: A greenhouse can be modeled as a rectangular prism with a half-cylinder on meridian. The rectangular prism is 20 feet broad, 12 feet high, and 45 anxiety long. The half-cylinder has a bore of 20 anxiety. To the nearest cubic foot, what is the book of the greenhouse?

Answer: The book of the rectangular prism section is:

Length x width x height

= 45 x 20 x 12 = 10800 cubic anxiety

The book of a cylinder is the cross-exclusive area x length

The cross-sectional area is the area of a circle

Let R be the radius = 20/2 = 10

and 50 exist the length = 45

Expanse = πR²

Book = πR²L

For a half cylinder

Volume = πR²L/2

= 3.1416 (10)² x 45/2 = 7069 cubic feet to the nearest cubic human foot

Full volume = 7069 + 10800 = 17869 cubic feet

Question: What is the maximum and minimum value for the sine of an angle?

Answer: If θ is the angle, the maximum value of sine occurs when θ = ninety degrees or π/2 radians. The minimum value is -one and this occurs when θ = 270 degrees or 3π/2 radians.

Question: How do I know when to use the sine or cosine formula?

Answer: If you know the length of 2 sides and the angle between them, and so you can use the cosine formula to work out the remaining side. Otherwise, the sine formula or Pythagorean theorem can be used.

Question: How exercise you solve the side lengths (given only their algebraic values - no numerical ones) and the 90 degree angle?

Answer: Apply the sine dominion, cosine dominion and Pythagoras theorem to express the sides in terms of each other and solve for the unknown variables.

Question: How do y'all find the length of all the sides of a right triangle if all you know is Cos B is 0.75?

Answer: You can find the angle B from the arccos of 0.75 and and then use the fact that the 3 angles add upwardly to 180 to discover the remaining bending. However there is an infinite number of similar right triangles that have all three angles the same, then you need to know at least the length of one side.

Question: Which formula is used when given 90-degree triangle, contrary angle is 26 degrees and one leg is know?

Reply: Use the fact that the cos of an angle is the length of the adjacent side divided by the hypotenuse, or the sine of an angle is the reverse side divided by the hypotenuse. In your example, you know the side contrary the angle.

So sine (26 degrees) = length opposite side / length hypotenuse

Therefore

Length hypotenuse = length reverse side / sine (26 degrees)

Utilise Pythagoras'due south theorem to work out remaining side

and remaining bending = 180 - (90 + 26) = 64 degrees

Question: How do I find the angles of a triangle if I know the lengths of all three sides?

Answer: Use the cosine rule to find 1 of the angles. You'll demand to utilize the arccos or inverse cos function to work out the value of the angle. Then apply the sine rule to find another bending. Finally, use the fact that the sum of the angles is 180 degrees to detect the remaining third angle.

Question: How do you detect the side of a right triangle given 2 angles and hypotenuse?

Answer: If you know 2 angles, then you tin work out the third since all the angles sum to 180 degrees. If the sides are a, b and the hypotenuse is c (opposite angle A), and the angles are A, B and C, then Sin A = a/c, so a = cSin A. Also Cos A = b/c, so b = cCos A.

Question: What rule would be used to detect the length of sides if all 3 angles are known?

Answer: In that location is an infinite number of similar triangles that have the aforementioned angles. Imagine if you have a triangle and you know all the angles. You lot tin can keep making it bigger, but the angles stay the same. However, the sides get longer. So you demand to know the length of at least one side. Then you tin use the Sine Dominion to work out the remaining three sides.

Question: ABC is a triangle in which AB=20 cm and bending ABC =30°.Given that the expanse of the triangle is ninety cm^2, find the length of BC ?

Reply: The formula for the expanse of the triangle is (i/2)AB X BCSinABC

So rearranging:

BC = surface area / (1/2)ABSin(ABC)

= 2area / ABSin(ABC)

Plug in the values to work out BC:

BC = two x 90 / (20 10 Sin 30)

Question: How do yous find an angle of an isosceles if you only know 2 sides and the area?

Answer: Permit the triangle accept sides of length a, b and c and angles A, B and C.

Angle A is opposite side a

Angle B is opposite side b

Angle C is opposite side c

The two equal sides are a and b and the angle between them is C

Area = (1/2)absinC

a, b and the surface area are known

So sin C = area / ((one/2)ab)

C = arcsin(area / ((1/two)ab))

A + B + C = 180

But A = B

So A + B + C = 2A + C = 180

So A = (180 - C)/2

Use the cosine rule to find length c

Question: How do I get the area of a scalene triangle if I have two sides and the angle between them?

Answer: Utilise the formula 1/2abSinC where a and b are the two sides and C is the bending between them.

Question: If I have a one length of a triangle and the other angles how do I detect the missing length using the sine method?

Respond: Telephone call the sides a, b and c and the angles A, B and C

a is known and likewise A, B and C

So the sine rule says that a/Sin A = b/Sin B and rearranging gives b = (a/Sin A)Sin B

Similarly a/Sin A = c/Sin C and rearranging gives c = (a/Sin A)Sin C

Question: How should I approach the problem - The triangles ABC and ACD are such that BC- 32 cm, Advertising - 19cm, CD - 28cm BAC - 74 ( bending ) and ADC - 67 ( angle )?

Answer: Use the cosine rule to piece of work out AC. Then the sine dominion to piece of work out the remaining angles/sides.

Question: How do I know when to use sine or cosine formula when given two degrees and 1 length?

Answer: If the length is reverse one of the known angles, yous can employ the Sine Dominion. If it isn't, yous can work out the 3rd angle since the three angles sum to 180 degrees. And so use the Sine Dominion. The Cosine Rule is usually used when you only have one angle between two known sides.

Question: Each of the equal angles in an isosceles triangle measures 36 degrees. What is the measure of the third angle?

Answer: All the angles in a triangle add upward to 180 degrees. Both angles are 36 degrees so that'due south 72 degrees. The remaining angle is 180 - 72 = 108 degrees.

© 2016 Eugene Brennan

Eugene Brennan (author) from Ireland on July 03, 2020:

Hi Jacob,

If yous 2 angles, you can calculate the 3rd ane because all angles sum to 180 degrees. Then you need at least one side length and yous can use the sine rule to calculate the others.

Jacob Halstead on July 03, 2020:

Finding lengths of a trisngle's sides using two base of operations interior angles?

Eugene Brennan (writer) from Republic of ireland on June 05, 2020:

Howdy Swetha,

You need to know the length of at least i side. In that location are an space number of right angle triangles with the same three angles (similar triangles).

If you know ane side, yous tin can use sine and cos to work out the other sides.

Swetha on June 05, 2020:

How to find iii sides when angles are given in a right bending triangle.Give a formula to solve it?

Eugene Brennan (author) from Ireland on June 02, 2020:

Hi Kayla,

Draw your triangle with the side 8cm equally the base. Call this a.

Then describe side c at an angle of 45.5 to side a starting at the left of a. This is angle B. You don't know it'due south length, so just continue on the line

Depict side b starting at the correct of the base a. Y'all don't know the length of b either, so simply go along it on to intersect side b.

Employ method 2 above for area to first find the length of side c.

Then area = 1/2 air-conditioning sin B = 1/ii (8) c sin 45.5 = 4c sin 45.5 = 18.54 square cm

Rearranging gives c = 18.54 / (iv sin 45.5)

When you work out this value for c, y'all can use the cosine rule to notice the length of the side b opposite the 45.5 degrees angle. At present you know the lengths of all the sides so yous can use the sine rule to work out the angles.

Kayla on June 01, 2020:

Can yu please explain this question?

A triangle has 1 side length of 8cm and an adjacent angle of 45.v. if the area of the triangle is 18.54cm, calculate the length of the other side that encloses the 45.5 angle

Thanks

Eugene Brennan (writer) from Ireland on May thirteen, 2020:

How-do-you-do,

Then call the sides a, b and c and the angles A, B and C and assume the sides are a = 5 units, b = 7 units and c = 8 units. Information technology doesn't affair what the actual lengths of the sides are considering all like triangles accept the same angles. So if we work out the values of the angles for a triangle which has a side a = v units, it gives us the result for all these like triangles.

Utilise the cosine rule. So c² = a² + b² - 2abCos C

Substitute for a,b and c giving:

8² = 5² + 7² - 2(5)(vii)Cos C

Working this out gives:

64 = 25 + 49 - 70Cos C

Simplifying and rearranging:

Cos C = one/vii and C = arccos(1/vii).

Yous can utilise the cosine rule again to find a second angle and the third bending can be establish knowing all the angles add to 180 degrees.

Hello on May 13, 2020:

Can I detect sinus of the biggest or the smallest angle, if the merely thing I know is that the triangle is acute and it's sides are proportional to 5:vii:8?

Eugene Brennan (author) from Ireland on May 10, 2020:

Hullo Abike,

No, considering, there are an infinite number of combinations of angles for the other two angles or 2 sides.

Draw two lines with the known angle between them. Y'all'll see that y'all can make the ratio of their lengths anything you want, changing the angles also and so that one is big and the other pocket-sized or vice versa.

Abike on May 10, 2020:

Hello,

Is it possible to find the angles of an astute triangle with merely one known bending and no known side?

Eugene Brennan (author) from Ireland on April 29, 2020:

Use the simple formula:

expanse = one/ii the base x height

Multiply both sides of equation by 2

2area = ii ten ane/2 x base of operations x height = base past superlative

Dissever both sides by height

2area/height = base x height/height = base

and switch effectually the two sides

and then base of operations = 2area / top.

Suzy on April 28, 2020:

Find the length of the base. Where the height is 8 and the surface area is xx. Solve for the length base?

Emmy on April 07, 2020:

Thank you and so much!

Himanshu gond india on March 12, 2020:

Thanks a lot sir

Eugene Brennan (writer) from Ireland on February 27, 2020:

Hi Hassan, if we don't know the length of the side c, nosotros demand to know an boosted piece of data, the angle betwixt side a and b or 1 of the other angles.

Hassan on Feb 27, 2020:

Mr. Brennan, if nosotros have just ii side information for case a=five, b=10, and we know nothing about the angles so how to calculate c and any angle. the triangle is not right triangle.

Eugene Brennan (writer) from Ireland on February 20, 2020:

No problem Bob, glad to help! Have a great day besides!

Bob longnecker on February xx, 2020:

Mr. Brennan

Cheers very much. This is what I was looking for.

Have a great solar day and best regards .

Bob 50.

Eugene Brennan (author) from Ireland on February xx, 2020:

Howdy Bob,

The length of the curt side is 3.6" ten tan(30) which works out at 2.08" approx.

If the bending changes to 31 degrees, the short side is 3.6" ten tan(31) = ii.16" approx.

So the length variation of the brusk side would vary with the tan of the angle. If you lot await at the graph of tan, in that location's an approximately linear variation upwards to nearly 45 degrees (so the long side increases proportionately with the angle). So the graph gets steeper at an increasing rate, so the brusk side would change a lot for pocket-size variations of angle.

Bob longnecker on February xviii, 2020:

The 3.six side is reverse the threescore° bending. The 3.half-dozen side is the longest of the two short sides. I don't care about the hypotinuse. Just desire to really see what a change in the thirty° bending does and how it affects the curt side. First I demand the length of that side and and so the length of that side when I change the xxx° angle to 31°. How much does 1° change touch the length?

Eugene Brennan (author) from Ireland on Feb xviii, 2020:

In your first trouble Bob, which angle is the iii.6" length contrary? (or is this side the hypotenuse, the longest side?)

Bob longnecker on February 17, 2020:

However trying but no luck!

Eugene Brennan (author) from Ireland on February 17, 2020:

You lot can also apply a triangle reckoner like this i and all y'all have to practice is input values for side length and angle. If you lot have sufficient information, it will calculate the remaining sides and angles.

https://www.calculator.net/triangle-figurer.htm...

Eugene Brennan (author) from Republic of ireland on Feb 17, 2020:

If the triangle is right angled, and then:

sine (angle) = length of side opposite angle / length of hypotenuse

Therefore length of side opposite angle = length of hypotenuse ten sine(angle)

Similarly cos (angle) = length of side side by side to bending / length of hypotenuse.

Therefore length of side adjacent to angle = length of hypotenuse x cos(bending)

Tan(angle) = length of side opposite angle/length of side adjacent.

And then if you know all the angles (which you practise), and ane side, you can work out the remaining sides.

Bob longnecker on February 17, 2020:

Lamentable to say I'm 77 years onetime. I took trig and calc as a senior in high school "lx" years ago. Learning it taught me how to retrieve and trouble solve in life dorsum so but never used it Perdue afterward that. Forgot what I learned back so.

Do have a valid reason for the reply just don't have the wearable with all to go back and learn trig again.

What I actually need to know is how much B changes per degree of change in the hypothesis. Example going from 30 to 31°how much increment in B length ? What is your calculated answer.

Sorry just too tired to get back and visit sixty years ago when I was 17!

Thank you and best regards,

Bob longnecker

Eugene Brennan (author) from Republic of ireland on February 17, 2020:

Howdy Bob, you tin can use the sine, cos and tan relationships to work out bug like this.

Bob longnecker on February 17, 2020:

I have a triangle with angles of: 30,60 and 90°. Side A is know to be iii.6". I want to know what curt side B is. Tin can anyone give me the answer?

Problem #two.

I take a triangle with angles of 31, 59, and 90°. Long side A is iii.6". I want to know the length of curt side B.

Hi on Feb 12, 2020:

solve ii triangle and 4 triangle in quadrilateral by apply of sine rule

a/sin A= b/sinB that i know

Simply

a = sin A/ sinB what is that formula

I don't sympathize that formula only that true

Duran on January 22, 2020:

Hi Mr. Brennan.

I have a problem that is difficult for me:

Known:I have two angles:∠A and ∠B then I take a package of similar triangle-ABCs. At present at that place must be a betoken T within the triangles who forms three new sides: TA, TB and TC. I know that the angles betwixt all these three sides are equally 120 deg.

Q: Can I solve the angle-BAT.

That realy dislocated me for a while !

Eugene Brennan (author) from Ireland on Jan 04, 2020:

If the angle is 45 degrees, the remaining bending is also 45 degrees, so the triangle is isosceles likewise as being right angled. Then if the length of the hypotenuse is a and the other two sides are b and c, then from Pythagoras'due south theorem:

a^two = (b^2 + c^two) = (2b^2)

so b^2 = (a^2)/two

and b = c = a / square root of two

Nathaniel Gloyd on Jan 04, 2020:

If you have a right angle triangle, how would you discover the distance from the corner of the 90 degree, to the hypotenuse on a 45 degree angle

Eugene Brennan (author) from Ireland on December 19, 2019:

Hi Rj,

Use the sine rule.

So if your sides are a,b and c and you know their lengths and your angles are A, B and C and you know one bending A, then:

a/sin A = b/sin B

Turn both sides of the equation upside downwardly, and then:

sin A / a = sin B / b

Multiply both sides by b

b sin A / a = sin B

Piece of work out b sin A /a on your calculator and this gives you sin B.

Then take the arcsin of the upshot to become B. Once you have A and B, add and subtract from 180 to get C.

Rj on Dec nineteen, 2019:

If one angle and all three sides of the scalane triangle is given then how volition you get the measure of

other two angle

Eugene Brennan (author) from Ireland on Oct 24, 2019:

Hi Natalia,

Await at method 2 in the tutorial for finding the area of a triangle.

So the area is one/2 the product of ii sides multiplied by the sine of the bending between them.

In your question the sides are PQ and QR and the bending between them is PQR.

So area = (1/2) PQ sin PQR

Substitute for P, Q, angle PQR and the expanse:

xiv.two = (1/2) x 7 10 5 x sin PQR

Rearrange:

sin PQR = fourteen.2 / ( (1/two) x seven x 5 )

Take the arcsin of both sides. You can exercise all this on a calculator, but take care entering all the brackets and numbers considering it's very easy to make a error. Brand sure the calculators is set to "DEG" and employ the sin ^ -i (usually shift on sin) to work out arcsin.

I would recommend HiPer Calc as a good, free scientific calculator app for Android if you accept a smartphone.

PQR = arcsin (fourteen.two / ( (1/ii) x seven x 5 ) ) = 54.235° = 54° xv' approx

natalia on October 24, 2019:

Hi EUGENE, tin you lot solve this trouble for me and provide me with working out.

the area of triange PQR is 14.2cm squared, notice bending PQR to the nearest infinitesimal, given PQ is 7cm and QR is 5cm.

Eugene Brennan (author) from Ireland on October 09, 2019:

Howdy Pavel,

By diagonal, I presume you mean the hypotenuse.

So you can use Pythagoras' Theorem.

The square on the hypotenuse equals the sum of the squares on the other two sides.

Foursquare the 2 sides and add together:

(n + iv)² + 16² = (n + 8)²

Expand out:

northward² + 8n + sixteen + 256 = northward² + 16n + 64

Rearrange and simplify:

8n = 208

Giving n = 26

So the two sides are northward + 4 = xxx cm and n + 8 = 34 cm

Pavel on October 09, 2019:

I have a trouble almost a question tin can you lot help me please?

I have a right angled triangle the bottom line is sixteen cm the one on the side is due north+iv and the diagonal line is n+eight can you help me find the ii sides please?

Eugene Brennan (author) from Ireland on September 28, 2019:

Hi Carcada. You tin't. You can take as many triangles as you want with exactly the same iii angles. These are chosen like triangles. You need to know at least the length of one side, and then you can utilise the sine rule to work out the others.

Carcada Keischa on September 28, 2019:

if only the angles of each side of the triangle is given then how can we find the length of each side of the triangle?

Eugene Brennan (author) from Ireland on September 08, 2019:

You don't have plenty information. You need to have at least i of a, c, A or C.

Sin B = 1/ sqrt iii, simply gives you the angle B = (acos (1/sqrt 3)). Then if a is the base, side c tin can be any length without knowing the other sides/angles.

Hannah Adams on September 07, 2019:

I have a question. How do I find the missing sides of a triangle if I know that sin B=1/sqrt 3 and a=2

Eugene Brennan (writer) from Ireland on August fourteen, 2019:

tan (ɵ) = opposite / adjacent so opposite = side by side 10 tan (ɵ)

Now you know the opposite and side by side sidfes, utilize Pythagoras' theorem to piece of work out the hypotenuse.

Phoebe on August 13, 2019:

Hey, i have a triangle, all that is known is the adjacent, the right angle and the theta, how exercise i figure out the other sides,

asaba charles on July 23, 2019:

thank you

Maribel Gibbs from Paoli, Pennsylvania on May 22, 2019:

Wow, amazing! One of the best works I ever have seen hither!

Khaleel Yusuf on May 18, 2019:

A good review of many years of wining and dining with math calculations. Awesome!

Ur mum gay on Apr 24, 2019:

This is a decent website

Christopher on March 26, 2019:

Wow this is really helpful thanks

Michael on Jan xx, 2019:

Hi,

I'm wrapping my head around this problem: I know 1 side, and the ii angles produced by the median on the opposing corner. I'd like to know the length of the other two sides. I drew a scheme, bachelor here:

world wide web.Stavrox.com/image/Triangle.png

The dark-green values are known (a, blastoff, beta) , I'd like to calculate b, c and besides x. Tin can you assist me.

Ferny Vise from San Francisco, CA on January 19, 2019:

I really like this article. As a math major myself, I believe math is cute!

Oscar Skabar on December 02, 2018:

I accept an example I cannot work out..... Ii birds sitting on a 90 caste mask ane at 9m upwards & the other at 6m upward but are 15m autonomously from each other, they see a fish in the h2o, how practise I calculate the distance of the fish from the birds so they are equal in distance

Rodrigo on November 19, 2018:

Hullo, Eugene! You can calc the three angles inside a triangle using tangent half-angle similar this:

tan(blastoff/two) = r / (p-a)

tan(beta/ii) = r / (p-b)

tan(gamma/ii) = r / (p-c)

p = (a+b+c) / 2 (semiperimeter)

r = sqrt( (p-a)(p-b)(p-c) / p )

alpha + beta + gamma = 180 (they are the internal angles of the triangle :)

Congrats for your site!

Eugene Brennan (author) from Ireland on November eighteen, 2018:

Hi Carla. There may be a simpler fashion of doing it, but you tin can use the cosine dominion in contrary to work out the angle B. Then since it's bisected, you know half this angle. Then use the cosine rule in reverse or the sine rule to work out the angle betwixt sides AB and CA. You know the third angle (between the bisector line and side CA) because the sum of angles is 180 degrees. Finally use the sine dominion over again to piece of work out the distance from A to the bisection point knowing the length of AB and half the bisected angle.

Eugene Brennan (author) from Ireland on Nov 05, 2018:

You lot can't find side lengths with angles solitary. Similar triangles have the same angles, but the sides are unlike. You must have the length of at least one side and 2 angles.

william on Nov 05, 2018:

how do yous discover side lengths with but bending measurements

Eugene Brennan (author) from Ireland on November 03, 2018:

If you have the angle at each finish, then yous can piece of work out the tertiary angle because you know all the angles add upwards to 180 degrees. And so use the sine dominion to work out each side (see instance above in the text)

Karen on November 02, 2018:

i accept the the length of 1 side and the angle at each cease, what is the sum to piece of work out the length of the other sides

Eugene Brennan (author) from Republic of ireland on November 02, 2018:

Hi Tom,

If you know the lengths of all three sides, use the cosine rule first and the arccos function to work out one of the angles. Then use the sine dominion (or the cosine rule again) to work out the one of the other two angles and the fact that they add up to 180 degrees to find the last bending

Equally regards Excel, I've added a photograph to the article showing how to implement a formula for working out an bending using the cosine dominion.

tom sparks on Oct 23, 2018:

I have a right angled triangle and know the lengths of all three sides. I would like to calculate the other angles.

I have tried TAN in Excel just information technology says using this 'Returns the tangent of the given bending,.

What would be the best way to piece of work this out

Hope you tin assist

Kind regards

Eugene Brennan (author) from Ireland on Oct 21, 2018:

You need more information, either some other side or angle to solve.

Sanjeev on October 21, 2018:

Correct angle and h is 421.410

How find ii angles and two sides.

Eugene Brennan (author) from Ireland on September 28, 2018:

You kneed to know at least 1 other angle or length. The exception is a correct-angled triangle. If you know one angle other than the right angle, and so you can work out the remaining angles using sine and cos relationships between sides and angles and Pythagoras' Theorem.

SUDHAKAR G on September 28, 2018:

how to i observe the length in a Scalene triangle? nosotros konw only one bending and 1 length.

Eugene Brennan (author) from Republic of ireland on August 25, 2018:

If two sides are given and the angle between them, utilize the cosine dominion to observe the remaining side, so the sine rule to find the other side.

If the bending isn't between the known side, utilise the sine rule to find the angles first, then the unknown side.

You at least need to know the angle between the sides or i of the other angles and so in your instance it's the sine dominion you need to utilize.

Akhyar on Baronial 24, 2018:

If only two sides are given of a non right angled triangle .. then how to find bending between them

Eugene Brennan (author) from Republic of ireland on July 19, 2018:

Howdy Imran,

There'due south an infinite number of solutions for angles A and B and sides a and B. Draw it out on a piece of paper and you'll see that yous tin can orientate side c with a known length (east.g. choice a length of 10 cm) and alter the angles A and B to what always you want.

You need to know either the length of i more side or one more bending.

Imran Hussain from India on July 19, 2018:

Call the angles A,B and C and the lengths of the sides a, b and c.

a is contrary A

b is opposite B

c is opposite C

C is the right angle = 90º and c is the hypotenuse.

How to find the sides of triangle a and b and other 2 angles A and B, if i know just angle C and side c which is hypotenuse?

Eugene Brennan (author) from Republic of ireland on May 28, 2018:

Hullo Liam,

You need to know at least one of the sides.

You could have a very big or very small triangle with the same angles. These are chosen similar triangles. See the diagram in the tutorial.

Liam on May 27, 2018:

How do I find a side in a right angle triangle if I know all three angles merely no sides?

Eugene Brennan (author) from Ireland on May 24, 2018:

If the holes are equally spaced around the imaginary circle, and so the formula for the radius of the circle is:

R = B / (2Sin(360/2N))

Where R is the radius

B is the distance between holes

N is the number of holes

Divya on May 24, 2018:

how to calculate altitude of each hole at PCD from centre circle

Amar36 on Apr 17, 2018:

How-do-you-do sir

how is that possible to know bending by just having ratios of ii heights of triangle and u need non apply protector or some other instruments and not fifty-fifty inverse trigonometric functions but merely by ratio do we summate them or not if and so how

I asked it considering how they have founded the angles of dissimilar triangles with information technology any discovery of inverse trigonometric functions.

Thank in accelerate

Eugene Brennan (author) from Ireland on Feb thirteen, 2018:

No enough information shahid! If you retrieve nearly it, in that location's an infinite number of triangles that satisfy those atmospheric condition. Surface area = (i/2) base x acme. So there's no unique values of base and summit to satisfy equation (1/2) base x summit = ten thousand squared.

shahid abbasi on Feb thirteen, 2018:

area of correct angle triangle is 10m and ane angle is 90degree so how summate three sides and another two angles.

Eugene Brennan (author) from Republic of ireland on January 14, 2018:

If yous assign lengths to all sides, you lot easily can work out the angles. Which sides did assign a length to?

Gem on January xiii, 2018:

Any luck Eugene? I take figured out some of the angles by folding a role of the newspaper that can let me use trig to figure it out if I assign each side a length.

Eugene Brennan (author) from Ireland on Jan 07, 2018:

Hi Danya,

Because you know 2 of the angles, the third angle can simply be worked out by subtracting the sum of the 2 known angles from 180 degrees. Then use the Sine Dominion described above to work out the two unknown sides.

danya61 on January 07, 2018:

Howdy

I have a triangle with two known angles and one known length of the side between them, and there is no right angle in the triangle. I want to calculate each of unknown sides. How can I practice that? (The angle betwixt unknown sides is unknown.)

Eugene Brennan (author) from Republic of ireland on Jan 04, 2018:

Depict a diagram jeevan. I can't really visualize this.

jeevan on January 04, 2018:

there are 3 circles i large circumvolve is a pitch circle having 67 diameter and medium circumvolve is drawn on the circumference of pitch circle at the bending of v degree hvaing eleven.04 radius and a small circumvolve with just moves in x y direction on pitch circle radius having 1.5 radius and so if the medium circumvolve is moved 5degree so at which point the small circle is coinciding and the distance from small-scale circumvolve to eye of large/pitch circle.?

sir please assistance me finding the answer thank you.

Gem on December 29, 2017:

It is tough to prove for certain. I thought I had it by assigning each side a random length ( such every bit 2cm) and then taking the heart point as half, which looked similar the right angle triangle on the top right paw side was half of the half. But information technology still tin can't be proven to be one-half because of the fold.

Eugene Brennan (author) from Ireland on December sixteen, 2017:

If it's an equilateral triangle, the sides and angles tin be easily worked out. Otherwise the triangle tin have an infinite number of possible side lengths equally the apexes A and C are moved around. And so if none of the magnitudes of lengths are known, the expression for lengths of sides of the triangle and its angles would have to be expressed in terms of the square'southward sides and the lengths AR and CP?

Gem on December fifteen, 2017:

The whole trouble has no measurements or angles. It only has angle names such as A,B,C,D etc. My starting point is from the mutual knowledge that a foursquare has iv x xc degree angles. If I could determine i other angle then I could figure out the whole problem by using the 180 degree rule of triangles. I will snap a moving picture of information technology and attempt and upload it here on Monday, or sketch and upload it. It seems to be a real stumper, 2/lxx people at a workshop were able to figure it out, as I was told by the person who passed it along to me. I appreciate your answer, and I look forward to sharing the appropriate visual information with you.

Eugene Brennan (author) from Republic of ireland on Dec xv, 2017:

How-do-you-do Precious stone,

Is any information given nearly where the corners of the triangle touch the sides of the foursquare or the lengths of the foursquare'southward sides? If the triangle isn't equilateral (or even if it is), it seems that there would exist an infinite number of placing the triangle in the square.

Jewel on December fourteen, 2017:

Problem: A triangle is placed within a square. The triangle doesn't have measurements or whatever listed angles. And then we can't identify the blazon (although it looks equilateral) or make whatsoever concrete assumptions about the triangle. I'm suppose to figure out the angles of the triangle without a protractor or ruler based on the only angles I am given which are the 90 degrees from each corner of the square information technology's in. Since the lines that cutting through the square from the principal triangle inside the square make new sets of smaller triangles, I still can't make out gratuitous or supplementary angles since most of those smaller triangles aren't definitely right angles isosceles triangles.

I'm non sure if my question is clear, so if you answer back I'll endeavour and add a film or sketch to analyze.

Just moving-picture show a square with a triangle in it touching all three sides of its points to the square with no units of mensurate and no angles. We tin can just assume that the foursquare has 90 degree angles in the corners and that's all we are given to work with.

Thanks Gem

Eugene Brennan (author) from Ireland on December 01, 2017:

How-do-you-do Maxy,

Call the angles A,B and C and the lengths of the sides a, b and c.

a is opposite A

b is opposite B

c is opposite C

C is the right bending = 90º and c is the hypotenuse.

If the angle A is known and the side contrary information technology, a, is known

Then Sin A = opposite/hypotenuse = a/c

So c = a/Sin A

Since you know a and A, you can work out c.

And then use Pythagoras'southward theorem to work out b

c² = a² + b²

So b² = c² - a²

So b = √(c² - a²)

If the angle A is known and the side adjacent to it, b, is known

Then Cos A = side by side/hypotenuse = b/c

So c = b / Cos A

Since you know b and A, you tin can work out c.

Then use Pythagoras's theorem to work out a.

c² = a² + b²

So a² = c² - b²

So a = √(c² - b²)

Eugene Brennan (author) from Republic of ireland on November 27, 2017:

You need to use the cosine rule in reverse.

So if the angles are A, B, and C and the sides are a,b and c.

Then c² = a² + b² - 2abCos C

Rearranging gives angle C = Arccos ((a² + b² - c²) / 2ab)

Y'all can work out the other angles similarly using the cosine rule. Alternatively use the sine rule:

So a/Sin A = c/Sin C

So Sin A = a/c (Sin C)

and A = Arccos ( a/c (Sin C) )

and similarly for the other angles

Hannah on November 27, 2017:

How do you find the angle if all three sides are given

Eugene Brennan (author) from Republic of ireland on November 25, 2017:

Polygons are a lot more complicated than triangles because they can have any number of sides (they do of class include triangles and squares). Likewise polygons can exist regular (have sides the same length) or non-regular (have unlike length sides).

Here's two formulae:

For a regular or non-regular polygon with n sides

Sum of angles = (due north-2) x 180 degrees

For a regular convex polygon (not like a star)

Interior angles = (1 - 2/due north) 10 180 degrees

Eugene Brennan (author) from Ireland on November 23, 2017:

Hullo Jeetendra,

This is called a scalene triangle. The longest edge of any triangle is opposite the largest angle. If all angles are known, the length of at least one of the sides must be known in guild to find the length of the longest edge. Since y'all know the length of an edge, and the bending opposite it, you tin can apply the sine dominion to piece of work out the longest edge. So if for case you know length a and angle A, and so you can piece of work out a/Sin A.

If c is the longest side,

and then a/sin A = c/Sin C ,

so rearranging,

c = a Sin C / Sin A

a, C and A are known, and so y'all can work out c

Jeetendra Beniwal( from India) on Nov 23, 2017:

If all three angles are given and so how we find largest edge of triangle,if all angles are acute

Eugene Brennan (author) from Ireland on July 21, 2016:

Thanks Ron, triangles are great, they crop up everywhere in structures, machines, and the ligaments of the man body can be thought of every bit ties, forming one side of a triangle.

Ron Bergeron from Massachusetts, United states of america on July 21, 2016:

I've always found the math backside triangles to be interesting. I'm glad that you lot ended the hub with some examples of triangles in every 24-hour interval use. Showing a practical use for the information presented makes it more than interesting and demonstrates a purpose for learning near it.

lollistakinquanded1938.blogspot.com

Source: https://owlcation.com/stem/Everything-About-Triangles-and-More-Isosceles-Equilateral-Scalene-Pythagoras-Sine-and-Cosine

Share this post